Number Gestures

Mathematics is the study of relationships. So, what is the relationship between this image and the number 330?
For the answer we go to the Grotte de Gargas, where we can see the panel below.
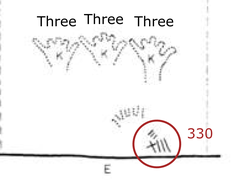
There are five examples of what Leroi-Gourhan classifys as digit combination K in the Grotte de Gargas. Three of them can be seen on this panel. Combination K is the number gesture for three. Similar gestures are still used by traders in China.
According to Leroi-Gourhan, the three hands are coloured red and are repetitions of the same person’s hand¹. He also states that many of the hands depicted are those of adolescents or children2.
My interpretation is 33 using three spaces on the counting board. In other words the number 330, which someone has thoughtfully written in Suzhou numerals beneath the hands. Perhaps the young people were learning how to use rod numerals.
Reading from top to bottom and right to left, in the area circled above, we have:
sān 三, three;
sān 〣, three, and;
shí 十, ten.
We can then use the hand gesture for three to determine the meaning of the other hand gestures shown in the table below.
Five of Mr Leroi-Gourhan’s digit combinations were not used. I have therefore blanked them out to avoid confusion. We are left with ten combinations. Furthermore, we know that most of the hands depicted are left hands. Hence, we need to count with the left hand. Starting with fingers raised, we lower the index finger first to give us one. Following through in sequence brings us to combination K, which is the hand gesture for three. At four we run out of fingers, so we start the next sequence by raising the index finger to get five. Two more raised fingers take us to seven. At this point, we need to be a little more inventive to get a unique combination of digits, so, with all fingers raised, we lower the middle finger to get eight. Lastly we lower the ring finger to get nine.
I don’t know whether there was the concept of zero. However, in Suzhou numerals zero was depicted as a blank. The starting hand (combination A) may therefore, perhaps be thought of as the blank, because no number is depicted. Interestingly, combination A appears at five metres above ground level in the second room of the cave3. Perhaps it was used to indicate that this was the place that the children came to learn about numerals.
Author's Notes
In the same way that the glyphs can have more than one interpretation, which depends upon context, I think that the painted hands may also have more than one meaning. For example, at the Grotte de Gargas combination N represents the number five, whereas in Grotte Cosquer, we see a similar hand used to indicate danger to the right.
I am not a mathematician. I would therefore like a mathematician to study Gargas. Is it possible to determine what the other panels say? I would expect that the colour coding and orientation of the hands are significant. I would suggest trying red for positive numbers, black for negative numbers, vertical hands for single digits, and perhaps horizontal hands for exponents. If the partial hands (knuckles and digit tips) are not merely remnants, but were painted that way, they too will have a meaning. In the past the thumb was a unit of measurement. On some of Mr Leroi-Gourhan’s drawings, the number of digit tips appears to equal the difference in value between nearby hands4.
References
All references are from: André Leroi-Gourhan: Les mains de Gargas. Essai pour une étude d'ensemble. Bulletin de la Société préhistorique française. Etudes et travaux, Année 1967, Volume 64, Numéro 1. From: http://www.persee.fr/web/revues/home/prescript/article/ bspf_0249-7638_1967_hos_64_1_4105: Accessed: 7 November 2012.
Image Credits:
Digit Combination K: André Leroi-Gourhan: p. 109 fig. 1 K.
Number 330: André Leroi-Gourhan: p. 116 fig. 6 E.
Number Gestures: André Leroi-Gourhan: p. 109 fig. 1.
Notes:
1. Repetition: André Leroi-Gourhan: p. 118 table.
2. Children: André Leroi-Gourhan: p. 118.
3. Combination A: André Leroi-Gourhan: p. 108.
4. Digit tips: André Leroi-Gourhan: p. 114 fig. 4, section 4, panel 15; p. 116 fig. 6, bottom panel.

 Cave Script
Translation Project
Cave Script
Translation Project
